Chapter 12: Relative motions of Sun & Earth
12.1 Introduction
Each year, planet Earth covers a distance of ~14036 km along its PVP orbit at the tranquil speed of 1.6 km/h. This distance amounts to 0.0039457% of the PVP orbit’s circumference of 355 724 597 km. From one year to the next, the Earth and the Sun will thus meet up at a slightly ‘earlier’ point in space, with the difference corresponding to a 0.0039457% slice of the solar orbit’s circumference.
Circumference of the PVP orbit = 355 724 597 km
Annual displacement of the Earth = 14036 km
14036 amounts to 0.0039457% of 355 724 597
The Sun’s orbital circumference = 939 943 910 km
Ratio between the Sun’s orbital diameter and the PVP orbit = 2.64233
Annual displacement of the Earth projected onto the Sun’s orbit:
14036 x 2.64233 ≈ 37088 km (0.0039457% of the Sun’s orbital circumference)
Fig. 12.1
In our epoch (J2000), the firmament is observed to drift ‘eastwards’ by about 50.3 arcseconds annually. However, as I will demonstrate below, the actual annual eastward drift of the firmament amounts to 51.136 arcseconds, i.e. ~1.68% more than the observable drift. In Chapter 11, we referred to this value as the ‘annual constant of precession’ (ACP).
ACP = 51.136″ (periodic) = 0.0039457% of 1 296 000″ (360°)
TYCHOS Great Year (TGY) = 25344 solar years
ACP x TGY = 1 296 000″ (360°)
In other words, the so-called Precession of the Equinoxes is caused by Earth’s clockwise motion around its PVP orbit.
12.2 The ‘sidereal day’ versus the ‘solar day’
We shall now see how the TYCHOS model accounts for the ‘sidereal day’ and the ‘solar day’. The Earth employs 23h56min to complete one 360° revolution around its axis and realign with a given star; this is known as the ‘sidereal day’. During that time, the Sun will move ‘eastwards’ in relation to the stars by about 1°. Hence, an earthly observer will have to wait another 4 minutes or so to realign with the Sun and complete a ‘solar day’ of 24h00min.
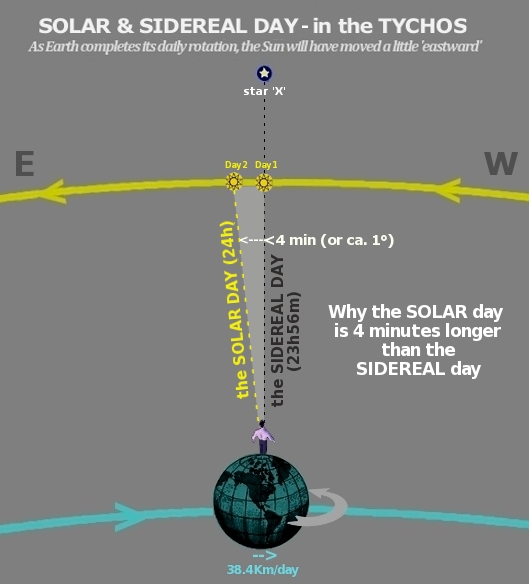Fig. 12.2 As the Earth completes its daily rotation, the Sun will have moved a little ‘eastward’. This is why the solar day is 4 minutes longer than the sidereal day.
I think you will agree the TYCHOS model accounts for the sidereal and solar days in the simplest manner imaginable. As we shall see shortly, the heliocentrists’ explanation for the sidereal and solar days is not only complicated; it is inherently unphysical.
'Unphysical': "Not supported by, or contrary to, the laws of physics." "unphysical" - Wiktionary's definition (opens in a new tab)
The Sun moves every day by about 1° (or 4 minutes of RA) in relation to the firmament.
This fact alone suggests that it is indeed the Sun and not the Earth that moves each day by 2 573 424 km, for this value equals roughly twice the Sun’s diameter of 1 392 000 km. Since the Sun’s apparent size in the sky subtends about 0.5°, it makes perfect optical sense that its observed daily displacement of about 1° corresponds to approximately twice its visible diameter.
Fig. 12.3 At the speed of 107226 km/h, the Sun will cover 2 573 424 km each day, almost twice its own diameter.
Let us now see if the notion that the Sun orbits around Earth can be further confirmed.
The Sun’s orbital circumference = 939 943 910 km
939 943 910 km / 1 296 000″ ≈ 725.265 km
The concept of ‘angular diameter’ is explained in the Wikipedia:
“An object of diameter 725.27 km at a distance of 1 AU (average Earth > Sun distance) will have an angular diameter of one arcsecond”. "Angular diameter" - Wikipedia (opens in a new tab)
Incidentally, this is why the observed solar parallax value is 8.794 arcseconds. If we take 8.794 and multiply it by 725.265 km, we get 6378 km (Earth’s radius). Therefore:
• Earth’s angular diameter (as viewed from the Sun) = 17.588” arcseconds (8.794 × 2 = 17.588)
The currently accepted value of solar parallax is 8.794143″. Let us calculate how many kilometers of the Sun’s orbital circumference is subtended by the ACP:
• Sun’s orbital circumference section subtended by the ACP ≈ 37088 km (51.136 × 725.27 ≈ 37088)
This is an excellent confirmation of our above estimate of 37088 km for the annual drift of the Sun’s position against the starry background (which, as we have seen, is caused by Earth’s annual displacement), representing 0.0039457% of the Sun’s orbital circumference. One could also put it this way: 51.136 arcseconds equals 0.05681 minutes of time, and 0.05681 x 25344 equals 1440 minutes (360°) (the celestial sphere is measured with a spherical ruler divided in 1440 minutes, or 24 hours).
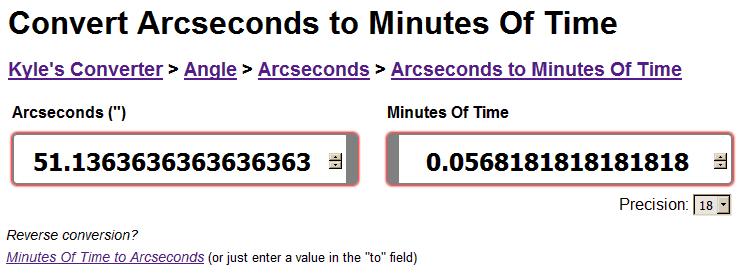Fig. 12.4 (Source: www.kylesconverter.com (opens in a new tab))
Once more, it would seem our value for the TGY (25344 years) holds up quite nicely. Next, let us unpack the heliocentrists’ unphysical explanation for the different lengths of the sidereal day and the solar day.
12.3 Solar versus sidereal day in the heliocentric model
Fig. 12.5 is a classic Copernican diagram intended to explain the sidereal/solar day discrepancy. Keep in mind that Earth is supposedly travelling over 2.5 million km every day, yet no parallax whatsoever is observed between the Sun and the stars at the completion of one sidereal day (23h56min). Once again, the Copernican explanation for this inconvenient fact is that “the stars are almost unimaginably distant”. However, if we take a closer look, this makes no optical sense. Earth is supposed to have moved some 2.5 Mkm between the positions of ‘Day 1’ and ‘Day 2’. But what exactly is implied by this Copernican diagram?
Fig. 12.5 Image source: The Solar and Sidereal Days - by A-star Maths/Physics Tuition/Tests/Notes (opens in a new tab)
To think that Earth would be moving by over 2.5 Million km each day without the background stars drifting by any noticeable amount besides these last 4 minutes of earthly rotation has to be among the most surreal aspects of the Copernican model!
Fig. 12.6 An observer at point A should expect the distant star to have drifted noticeably ‘eastward’ as point B is reached.
To put this problem in due perspective, observe the sidereal and solar day unfold in the 3 frames of Figure 12.7.
Fig. 12.7 The sidereal day (23h56min) vs. the solar day (24h00min) day, as depicted by the Neave planetarium.
The following description is what is observed, in reality, from one day to the next: In 23h56m, an earthly observer will line up again with the same given star. At such a point and time, the Sun will already have moved eastwards by approximately 4 minutes of RA. Four minutes later, we see the stars have drifted westwards by 4 min of RA. Ergo, the entire amount of our daily westward stellar drift will appear to an earthly observer to occur in the last 4 minutes of earthly rotation. In other words, Earth might just as well be stationary while only rotating around its axis. Many astronomers in ancient times believed this to be true, not because they were poor astronomers, but because this is what matches careful and patient observation of the Sun’s behaviour.
Of course, the TYCHOS model submits that Earth moves by a mere 38.4 km per day, which is hardly a noticeable amount of lateral displacement to the naked eye. Those 4 min of RA are the consequence of Earth having rotated by 360° in 23h56min, thus needing another 4 minutes to line up again with the Sun. Meanwhile, the Sun has moved eastwards by about 4 minutes of RA.
Instead, the Copernican theory would have us believe that Earth is moving each day by 2.5 million km with no amount of the observed daily 4-minute stellar drift optically attributable to this enormous displacement. It is as if the Earth’s rotation is the only thing that changes the star positions, while Earth’s alleged daily 2.5-Mkm displacement has no effect.
12.4 Solar versus sidereal year in the TYCHOS model
The sidereal year is 20.41 minutes longer than the solar (or ‘tropical’) year. This may seem counterintuitive, considering that the sidereal day is 4 minutes shorter than the solar day. As we shall see, this apparent contradiction turns out to be due to Earth’s 1-mph motion around the PVP orbit.
The Copernican model offers yet another incredibly convoluted explanation for this conundrum. If you are not familiar with it, you can go to sources like the Wikipedia or browse the example data compiled by Michael J. White, an Arizona State University professor of philosophy: "Sidereal, tropical, and anomalistic years" (opens in a new tab) by Michael J. White
In any case, the riddle is nicely summarised in this discerning question raised by the Binary Research Institute:
“Sidereal vs. Solar Time: Why is the delta (time difference) between a sidereal and solar day attributed to the curvature of the Earth’s orbit (around the Sun), but the delta between a sidereal ‘year’ and solar year is attributed to precession? (...) The burden of proof lies with those who support the current lunisolar precession theory which requires a different explanation for the two deltas.” "Understanding Precession of the Equinox: Evidence our Sun may be part of a long cycle binary system" (opens in a new tab) by Walter Cruttenden and Vince Dayes (2003)
Let us look at the math behind the time difference between the solar year and the sidereal year:
Average duration of a solar (or “tropical”) year: 365.24219 days - or 525948.753 minutes
Average duration of a sidereal year: 365.256363 days - or 525969.163 minutes
Difference: 20.41 minutes (0.00388%)
As shown above, 20.41 min is 0.00388% of 525960 min (365.25 days) and, in fact, the currently observed amount of annual equinoctial precession (50.29 arcseconds) amounts to 0.00388% of 1 296 000 arcseconds (a full circle). Hence, those 20.41 min are, manifestly, a direct consequence of the so-called equinoctial precession which, in the TYCHOS model, is caused by Earth’s orbital motion.
In the preceding chapter, we determined the annual constant of precession (ACP):
Currently observable annual precession rate = 50.29″
ACP = (50.29″ + 1.68%) = 51.136″
Note that the official estimate of the duration of one full 360° equinoctial precession (the Copernican Great Year) is ~25771 years. This is approximately 1.68% longer than the TGY (25344 solar years).
Figure 12.8 should help visualize why a small portion (~1.68% in our epoch) of the equinoctial precession will always remain unobservable from Earth. The ‘hidden angle’ of precessional drift can, without the slightest difficulty, be attributed to Earth’s orbital motion. To demonstrate this, let us first recall that Earth’s yearly displacement (14036 km), if projected unto the Sun’s orbit, corresponds to 37088 km. Travelling at 107226 km/h, the Sun covers ~36475 km in 20.41 min (0.3401667 hours). That is about 1.68% less than 37088 km.
Fig. 12.8 As Joe, our earthly observer, moves from A to B (from 21 June 2001 to 21 June 2002) he will have experienced a ‘solar year’. Since Earth has moved along by 14036 km in that same period, Joe will meet up with the Sun at an earlier point of the solar orbit in 2002. The Sun’s orbit being 2.64233 times larger than Earth’s PVP orbit, Joe’s lateral displacement will be proportionally equivalent to a 37088-km slice of the solar orbit (14036 x 2.64233 ≈ 37088 km). This is the distance between A and B.
It thus becomes plainly evident what causes this 20.41-min difference between the solar and sidereal year: it is simply the extra time needed for the Sun to realign with a given star, as viewed from Earth. These 20.41 minutes will effectively reset the Earth-Sun-star alignment which, in actuality, has been offset by Earth’s motion around its PVP orbit. To bring the point home, here is a description of the solar positions marked A, B and C in Figure 12.8:
The small angular offset with respect to the Sun-star alignment caused by Earth’s motion will quickly be ‘regained’ by the Sun’s speedy motion (107226 km/h). In only 20.41 minutes, the Sun will have lined up with the same star it faced one year earlier (point C). The distance between B and C is 36474 km, or 37088 km minus 1.68%.
Within Earth’s rotational frame of reference:
Daily rotation = 1440 min (or 1 296 000″)
1 min of rotation = 1 296 000 / 1440 = 900″
20.41 min of rotation = 20.41 x 900 = 18369″
Solar year = 365.25 days
Observed annual ‘equinoctial precession’ = 18369 / 365.25 = 50.29″
This explains why our earthly observer will not realize the full extent of the annual stellar precession: a small portion (~1.68%) will remain unobservable to him. Joe is unaware of Earth’s 1-mph motion and so mistakenly believes Earth has returned to the same physical location as the previous year. He will naturally conclude that the annual stellar precession rate amounts to 50.29″, rather than the actual annual constant of 51.136″ (ACP). Once again, the TYCHOS model provides a simple, rational and elegant explanation for a Copernican quandary, namely the fact that the sidereal year is longer than the solar year.
This further corroborates our demonstration in Chapter 10, showing that the observed precession has nothing to do with the heliocentrists’ hypothetical ‘lunisolar wobble’. As a final confirmation that these 20.41 minutes also correspond to a portion of the Earth’s axial rotation, we see that 18369” amounts to 1.4173% of 1 296 000” (i.e. 360°); as the Earth rotates at 1674 km/h, it will rotate by 568 km in 20.41 minutes. And in fact, 568 km amounts to 1.4173% of 40075 km (the Earth’s equatorial circumference).
12.5 About the ‘anomalistic’ year
The oddly-named ‘anomalistic year’ is the period required for the Sun to return to its closest or furthest point from Earth. On average, it lasts 365.259636 days, which is approximately 4.7 min longer than the sidereal year of 365.256363 days.
“The anomalistic year is usually defined as the time between perihelion passages. Its average duration is 365.259636 days (or 365 d 6 h 13 min. 52.6 s – at the epoch J2011.0).” "Anomalistic Year" - Wikipedia (opens in a new tab)
In the TYCHOS model, the anomalistic year might more aptly be described as “the time interval between the Sun’s perigee transits”. In our current epoch, the Sun’s perigee transit occurs around January 3rd. In short, the anomalistic year is determined by the Sun’s perigee procession. During those ~4.7 min with which the anomalistic year surpasses the sidereal year, a given point on Earth’s equator will rotate by 4230 arcseconds, as viewed within the terrestrial rotational frame of reference.
1 min of rotation = 1 296 000 / 1440 = 900″
4.7 min x 900″ = 4230″
Let us now imagine two hypothetical signposts (S and A) placed on the line of equator. The signposts are designed to slide along the equator according to the following parameters.
Signpost S (sidereal): Kept pointing towards a given star.
Signpost A (anomalistic): Kept pointing towards the celestial spot of each year’s passage of the anomalistic year.
Note that in this thought experiment we will disregard Earth’s daily rotation. Since signpost S is conceptually always being kept oriented towards a given fixed star, it will complete 1 revolution around Earth’s equator in 25344 years. On the other hand, signpost A will have moved each year by an extra 4230 arcseconds compared to signpost S. By the end of the TGY (25344 solar years), signpost A will have moved by 107 205 120 arcseconds.
4230 x 25344 = 107 205 120″
A/S spin ratio = 107 205 120 / 1 296 000 (full circle) = 82.72
Considering a spin ratio of 82.72, during 1 TGY (25344 solar years) signpost A will complete 82.72 times as many revolutions as signpost S. Since we know that signpost A moves by an additional 4230 arcseconds annually, we can calculate the annual displacement of signpost S:
4230 / 82.72 = 51.136″ = 1 ACP
You couldn’t make it up: the so-called anomalistic year, with its 4.7-min difference in relation to the sidereal year, corroborating the PVP orbit and its ACP value of 51.136 arcseconds!
As if that wasn’t good enough, there is yet another way of confirming the ACP value, namely by using the ‘progressive motion of the apogee in a year’, a parameter estimated at 11.75 arcseconds in the astronomy literature.
“On the anomalistic year: the year called the anomalistic year is sometimes used by astronomers, and is the time from the sun’s leaving its apogee till it returns to it. Now, the progressive motion of the apogee in a year is 11.75", and hence the anomalistic must be longer than the sidereal year, by the time the sun takes in moving over 11.75" of longitude at its apogee.” "The Elements of Astronomy: Designed for the Use of Students in the University" (opens in a new tab) by Samuel Vince (1811)
TGY = 25344 solar years
Progressive motion of the apogee in a year = 11.75″
Precession of the Sun’s apogee during 1 TGY = 25344 x 11.75 = 297 792″
Time required by the Sun’s apogee to complete a 360° precession = 1 296 000 / 297 792 = 4.35203094777 TGY
ACP = 4.35203094777 x 11.75 ≈ 51.136″
4.35203094777 TGY = 110297.87 years
This last value is only 0.6% smaller than what the value officially referred to as the ‘111000-year precession of the perihelion of Earth’s orbit’:
“The perihelion of the earth’s orbit, and of all the planets, is moving around the sun, and completes its revolution in 111,000 years.” "Foot Steps of the Ancient Great Glacier of North America: A Long Lost Document of a Revolution in 19th Century Geological Theory" - by Harold W. Borns Jr. and Kirk Allen Maasch (2015) (opens in a new tab)
Note the underlying absurdity of the above statement. Why would the Earth and all the planets share such a period and return to their respective perihelions in unison? It is obviously the orbital motion of the Sun (i.e. of its apsides) that displays this periodicity.
In the following two chapters, we shall be ‘howling at the Moon’ and the many lunar mysteries that have befuddled astronomers for millennia. As it is, the complexity of the Moon’s motions is, still today, a subject of intense study and unceasing reappraisal. So let us gather courage and see if the TYCHOS model can help us clear up this most perplexing affair.